Factorising
In algebra, factorising is the opposite of expanding.
It is useful to read the following guides before embarking on this topic.
Factorising expressions
We know that we can expand the expression \(2 (5q + 4)\) to give \(10q + 8\)
Expanding and factorising are inverse operations.
This means that we can factorise \(10q + 8\) to give \(2 (5q + 4)\)
To factorise an expression
- Look for a common factor and place this outside a bracket
- Work out what needs to go inside the bracket to keep the expression correct when multiplied out
- Keep the sign between the terms the same
Example 1
Factorise \(15 - 12m\)
Solution
Look for a common factor and place this outside a bracket.
Both 15 and 12 can be divided by 3.
3 goes outside the bracket.
\(15 - 12m = 3 (?)\)
Now, work out what needs to go inside the bracket.
\(15 Ă· 3 = 5\) and \(12 Ă· 3 = 4\)
Keep the sign between the terms the same.
Answer
\(15 - 12m = 3 (5 - 4m)\)
Check your work out by expanding.
\(3 (5 - 4m) = 15 - 12m\)
Question
Factorise \(14y - 35z\)
Solution
Both 14 and 35 can be divided by 7
7 goes outside the bracket.
\(14y - 35z = 7 (?)\)
Now work out what needs to go inside the bracket.
\(14 Ă· 7 = 2\) and \( 35 Ă· 7 = 5\)
The sign in the middle stays the same.
Answer
\(14y - 35z = 7 (2y - 5z)\)
Example 2
Factorise \(20n - 45\)
Solution
Look for a common factor and place this outside a bracket
The highest common factor of 20 and 45 is 5
\(20n - 45 = 5 (?)\)
Work out what needs to go inside the bracket
\(20 Ă· 5 = 4\) and \(45 Ă· 5 = 9\)
\(20n - 45 =5 (4n - 9)\)
Keep the sign between the terms the same
Answer
\(5 (4n - 9)\)
Check by expanding: \(5 (4n - 9) = 20n - 45\)
Example
Factorise this expression fully \(12 - 28p\)
Solution
A common factor of 12 and 28 is 2.
\(12 - 28p = 2 (6 - 12p)\)
While this statement is true, the expression has not be fully factorised.
To do this, the common factor outside the bracket must be the highest common factor and the numbers left in the bracket should not have any common factors.
The highest common factor of 12 and 28 is 4.
Answer
\(12 - 28p = 4 (3 - 7p)\)
Check by expanding: \(4 (3 - 7p) = 12 - 28p\)
Question
Factorise this expression fully \(32ab - 24c\)
Solution
The highest common factor of 32 and 24 is 8.
8 goes outside the bracket.
\( 32ab - 24c = 8 (?)\)
Now work out what needs to go inside the bracket.
\(32 Ă· 8 = 4\) and \(24 Ă· 8 = 3\)
\(32ab - 24c = 8 (4ab - 3c)\)
Answer
\(\mathbf {8(4ab - 3c)}\)
Check by expanding: \(8 (4ab - 3c) = 32ab - 24c\)
Test yourself
More on M1: Algebra
Find out more by working through a topic
- count2 of 7
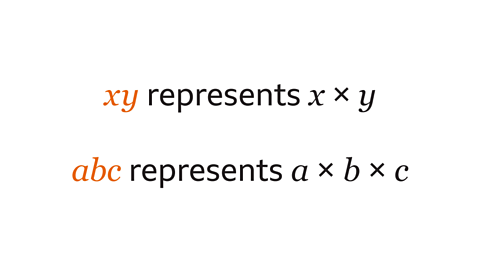
- count3 of 7
