Key points
A sequenceA sequence is a set of numbers that follow a certain rule. For example, 3, 5, 7, 9… is a sequence starting with 3 and increasing by 2 each time. is a list of numbers or diagrams that are in order.
Number sequences are sets of numbers that follow a pattern or a rule.
If the rule is to multiply or divide by a specific number each time, it is called a geometric sequence.
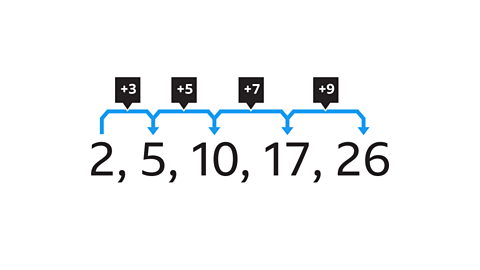
A number pattern which increases (or decreases) by the same amount each time is called an arithmetic sequenceAn arithmetic sequence is a sequence of numbers with a definite pattern. If you take any number in the sequence then subtract the previous one, the result is always a constant amount..
Recognising the pattern between the termAn element within an algebraic sentence. Elements (terms) are separated by + or - signs. means that the sequence can be continued using a term-to-termA term-to-term rule is a rule that allows you to find the next number in a maths sequence, if you know the previous numbers (or terms). rule.
Sequences that are connected by multiplicativeTwo numbers which are connected by multiplication. relationships are geometric sequences, whereas those connected by additiveThe same number is added each time to produce the next value. relationships are linear.

Finding missing terms in a geometric sequence
Each term in a geometric sequence is found by multiplying or dividing the previous term by the same amount, this is called the common ratio.
To find the common ratio, start by calculating the difference between each pair of numbers, moving from one term to the next.
Examples

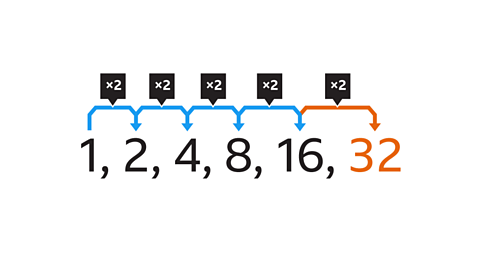
Image caption, What is the next term in the sequence?
Image caption, To work out the next term in the sequence, look at the difference between each pair of numbers. The difference between each pair of terms is a different amount each time. The difference between 1 and 2 is 1, the difference between 2 and 4 is 2, the difference between 4 and 8 is 4 and so on. The number pattern does not increase by the same amount each time. It is not an arithmetic linear sequence.
Image caption, Although the sequence is not arithmetic, there is a pattern between the difference of each pair of terms. If the pattern continues, the next difference will be +16. This means that the next term is 32
Image caption, Each term in the sequence is doubling (multiplying by 2) to create the next term. This is a multiplicative relationship. The term-to-term rule is √ó2
Image caption, As each term is multiplied (or divided) by the same number (2) to make the following term, this sequence is called a geometric sequence. The next term in the sequence will be 32 (16 x 2).
Image caption, What is the next number in this sequence?
Image caption, The common difference between a pair of terms is found by subtracting the smaller term from the larger term. 6 ‚Äď 2 = 4, 18 ‚Äď 6 = 12 etc. This shows that the sequence is not a linear arithmetic sequence.
Image caption, There is a multiplicative relationship between each pair of terms. Each term in the sequence is multiplied by 3 to create the following term. The term-to-term rule is √ó3. The sequence will continue in the same way, multiplying the previous term (54) by 3 will give the next term.
Image caption, The next term will be 162 (54 x 3).
1 of 9
Question
What is the next number in this geometric sequence?

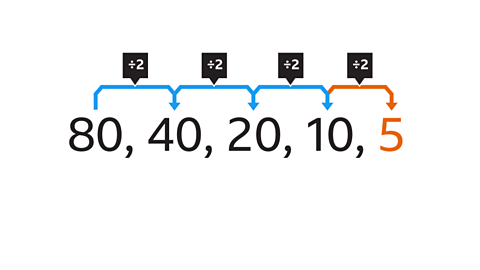
Each term in the sequence is divided by 2 to create the next term.
The next term in the sequence is found by dividing the previous term (10) by 2
10 √∑ 2 = 5
5 is the next number in this geometric sequence.
Finding the common ratio
The common ratio is the number you multiply or divide by at each stage of the sequence. It is found by dividing two consecutive pairs of terms.
It does not matter which pair of terms is chosen, as long as they are next to each other in the sequence.
Examples

Image caption, What is the common ratio of this geometric sequence of numbers?
Image caption, 100 multiplied by the common ratio gives the next term, 200. To calculate the common ratio, calculate 200 √∑ 100 = 2. This means that the common ratio is 2. 100 √ó 2 = 200, 200 √ó 2 = 400, 400 √ó 2 = 800
Image caption, What is the common ratio of this geometric sequence of numbers?
Image caption, The common ratio is found by dividing two consecutive pairs of terms. The first 2 terms in the sequence are 50 and 200. 200 √∑ 50 = 4, 800 √∑ 200 = 4 and 3200 √∑ 800 = 4. The common ratio is 4. The next term in the sequence is found by multiplying the last term by 4
Image caption, What is the common ratio of this geometric sequence of numbers?
Image caption, The common ratio is found by dividing two consecutive pairs of terms. The first 2 terms in the sequence are 4000 and 2000. 2000 √∑ 4000 = 0‚ąô5, 1000 √∑ 2000 = 0‚ąô5 and 500 √∑ 1000 = 0‚ąô5. The common ratio is 0‚ąô5. The next term in the sequence is found by multiplying the last term by 0‚ąô5
Image caption, Multiplying the last term by 0‚ąô5 will produce the next term. This relationship could be described using division as well as multiplication. Each term has also been divided by 2 to reveal the next term. 4000 √∑ 2000 = 2, 2000 √∑ 1000 = 2 and 1000 √∑ 500 = 2. The next term in the sequence is found by dividing the previous term by 2
Image caption, Multiplying by 0‚ąô5 and dividing by 2 produces the same answer. The next term in the sequence can be found by working out 500 x 0‚ąô5 or 500 √∑ 2. Both reveal that the next term is 250
1 of 8
Question
What is the common ratio of this geometric sequence?

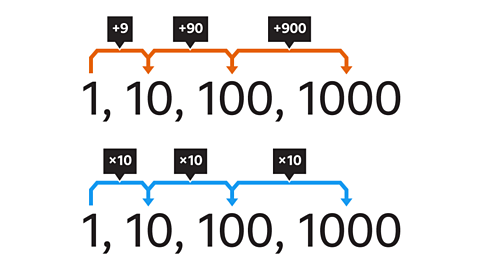
The common ratio is the number you multiply or divide by at each stage of the sequence.
The differences between the terms are not the same each time, this is found by subtracting consecutive terms.
The differences are 9, 90 & 900. This shows that it is not an arithmetic linear sequence.
The common ratio is found by dividing two consecutive pairs of terms.10 √∑ 1 = 10, 100 √∑ 10 = 10 and 1000 √∑ 100 = 10
The next term in the sequence is calculated by multiplying the last term by 10, so the common ratio is 10
Practise geometric sequences
Quiz
Practise recognising and finding terms in geometric sequences with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

Geometric sequences are used in everyday life when something follows a pattern. An example of this is in scientific work, when the growth of bacteria is monitored.
Bacteria, like penicillin, grow in a geometric sequence. Scientists, such as microbiologists, can predict how much bacteria will develop in a petri dish after a certain number of days by finding the common ratio.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from ≥…»ň¬ŘŐ≥ Bitesize.

More on Patterns and sequences
Find out more by working through a topic
- count4 of 4