Fractions
- Fractions can be added, subtracted, multiplied or divided.
- A fraction of an amount can be calculated.
How to add and subtract fractions
- To add/subtract fractions with the same denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1тБД3, the denominator is 3, add/subtract the numeratorNumber written at the top of a fraction. The numerator is the number of parts used. Eg, for 1тБД3, the numerator is 1 and keep the denominator.
- When fractions have different denominators, find a common denominatorA denominator that is the same for two or more fractions. and add/subtract the new numerators.
Example:
\( \LARGE \frac{2}{11}+\frac{5}{11}+\frac{1}{11}= {\color{red}{?}}\)
Showing your working out is essential to gain marks in questions like this
To add fractions with the same denominator, add the numerators and keep the denominator.
\(\LARGE \frac{{\color{red}{\textbf{2}}}+{\color{red}{\textbf{5}}}+{\color{red}{\textbf{1}}}}{11}=\frac{{\color{red}{\textbf{8}}}}{11}\)
Example:
\(\LARGE {4 \frac{2}{7}- 1\frac{5}{7}= {\color{red}{?}}}\)
Showing your working out is essential to gain marks in questions like this
Make the fractions top heavy and then subtract.
\(\LARGE {\frac{30}{7}- \frac{12}{7}= {\color{red}{\frac{18}{7}}}}\)
Change the answer back to a mixed number.
\(\LARGE {\frac{18}{7}= {\color{red}2{\frac{4}{7}}}}\)
Question:
\(\LARGE {\frac{8}{15}+\frac{11}{15}= {\color{red}{?}}}\)
Show your working
Solution:
\(\LARGE {\frac{8}{15}+\frac{11}{15}}=\color{red}{\frac {8+11}{15}}\)
\(\LARGE\color{red} = \frac{19}{15}\)
\(\color{red} = 1{\frac{4}{15}}\)
Answer:
\(\LARGE = 1{\frac {4}{15}}\)
Question:
Calculate the value of \(\LARGE 2{\frac{2}{7}}-1{\frac{4}{7}}\)
Show your working
Solution:
Make the fractions top heavy and then subtract.
\(\LARGE {\frac{16}{7}}-{\frac{11}{7}}=\color{red}{\frac {5}{7}}\)
Answer:
\(\LARGE = \frac {5}{7}\)
\( \LARGE {\frac{5}{4}+\frac{8}{3}}=\color{red}?\)
Show your working
When fractions have different denominators, find a common denominator and add the new numerators.
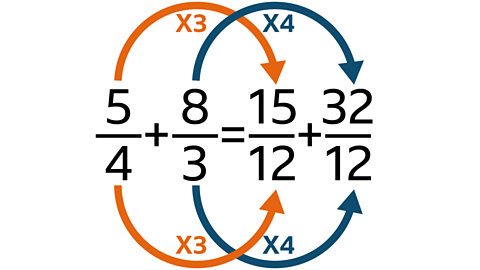
Now add the numerators
\( \LARGE {\frac{15}{12}+\frac{32}{12}}=\frac{47}{12}\)
And change the answer to a mixed number
\( \LARGE {\frac{47}{12}}= \color {red} 3 \frac{11}{12}\)
Question
Calculate the value of \( \LARGE \frac{5}{8}-\frac{1}{6}\)
Show your working
Solution
Find a common denominator
\(\LARGE {\frac{15}{24}-\frac{4}{24}}=\frac{11}{24}\)
Answer:
\(\Large \frac{11}{24}\)
Multiplying fractions
Fractions can be multiplied or divided.
How to multiply fractions
- Change any mixed numbers to top heavy fractions before multiplying.
- Multiply the numerators and then multiply the denominators.
- Write the answer in its simplest form.
Example
Showing your working out is essential to gain marks in questions like this
Calculate
\( \LARGE {\frac{2}{3} \times 2 \frac{1}{5}}\)
Change any mixed numbers to top heavy fractions
\( \LARGE 2{\frac{1}{5} = \color{red} \frac{11}{5}}\)
Multiply the numerators and then multiply the denominators
\( \LARGE {\frac{2}{3} \times \frac{11}{5} = \color{red} \frac{22}{15}}\)
Change \(\normalsize {\frac{22}{15}}\)into a mixed number
\( \LARGE {\frac{22}{15} = \color{red} 1\frac{7}{15}}\)
Question
Calculate the value of \( \LARGE \frac{5}{6}\times\frac{2}{3}\)
Show your working
Solution
\(\LARGE {\frac{5}{6}\times \frac{2}{3}}=\frac{10}{18}\)
\(\LARGE {\frac{10}{18}}=\frac{5}{9}\)
Answer:
\(\Large \frac{5}{9}\)
Dividing fractions
How to divide fractions
Change any mixed numbers to top heavy fractions then,
- KEEP the first fraction as it is
- CHANGE the ├╖ to a ├Ч
- FLIP the second fraction
Then multiply the fractions and write the answer in its simplest form.
Example
Calculate \( \LARGE {\frac{2}{3}\div\frac{3}{4}}\)
Remember to show your working
| \(\hspace{2em}{\color{red}\textbf{KEEP}}\) | \(\hspace{2em}\color{red}\textbf{CHANGE}\) | \(\hspace{2em}\color{red}\textbf{FLIP}\) |
| \(\hspace{3em}\LARGE\frac{2}{3}\) | \(\hspace{4em}\LARGE\times\) | \(\hspace{3em}\LARGE\frac{4}{3}\) |
Then multiply the numerators and then the denominators.
\( \LARGE {\frac{2}{3}\times\frac{4}{3}}=\color{red}\frac{8}{9}\)
Question
Calculate the value of \(\large\frac{3}{8}\div\frac{2}{5}\) showing your working out.
Solution:
| \(\hspace{2em}{\color{red}\textbf{KEEP}}\) | \(\hspace{2em}\color{red}\textbf{CHANGE}\) | \(\hspace{2em}\color{red}\textbf{FLIP}\) |
| \(\hspace{3em}\LARGE\frac{3}{8}\) | \(\hspace{4em}\LARGE\times\) | \(\hspace{3em}\LARGE\frac{5}{2}\) |
Answer:
\( \LARGE\color{red}\frac{15}{16}\)
Fractions of a quantity
To find a fraction of a quantity
- Divide the amount by the denominator.
- Multiply the answer by the numerator.
The multiplication and division can be done in either order.
Example
Calculate \(\frac{2}{3}\text {of } 27\) showing your working out.
Divide the amount by the denominator. \(27 \div 3 = \color{red}9\)
Multiply the answer by the numerator. \(9 \times 2 = \color{red}18\)
\(\large\frac{2}{3}\text {of } 27=\color{red}18\)
Question
Jacob got ┬г20 from his grandmother. He spent тЕЦ of this on a book.
How much did the book cost?
Solution:
Calculate тЕЦ of 20
\( \LARGE 20\div 5 = \color{red} 4\)
\( \LARGE 4\times 2 = \color{red} 8\)
Answer:
The book cost ┬г8
Test yourself
More on M2: Number
Find out more by working through a topic
- count2 of 6
- count5 of 6
