Why do you compare fractions?
Comparing fractions is important because it shows you how much of the whole is being represented within each fraction.
Imagine you were sharing a cake. You wouldn’t want someone to get a much bigger piece than you! When cutting cakes, you visually compare fractions to make sure everyone gets an equal slice.

The two types of fractions we are going to look at comparing are unit fractions and fractions with the same denominator.
Comparing unit fractions
A unit fraction is a fraction where the numerator is 1 (the denominator can be any other whole number). For example \( \frac{1}{4}\):

Since the numerator (top number) never changes with a unit fraction, you have to look at the denominator (bottom number) to compare two fractions.
The bigger the denominator, the smaller the fraction!
This is because if the denominator is higher, the whole has been split up into more parts.
Example 1
Which is bigger,\( \frac{1}{6}\) or \( \frac{1}{3}\)?
Since both fractions are unit fractions you have to look at the denominator to decide which fraction is bigger. You can also use bar models to help you compare.
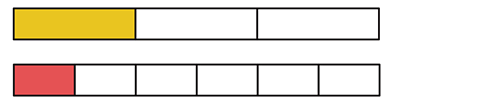
You can see that \( \frac{1}{3}\) is the bigger fraction because it has been split up into fewer parts.
If we used the greater than and less than signs, we would write:
\( \frac{1}{3} > \frac{1}{6}\)
Comparing fractions with the same denominator

It is easy to compare fractions with the same denominator. You only have to focus on the numerator.
The fraction is larger if the numerator is a bigger number. That’s because you are talking about more parts of the whole.

Example 2
Luke and Khadija cut a pizza into 6 slices. Luke ate \( \frac{2}{6}\) of the pizza and Khadija ate \( \frac{3}{6}\). Who ate more pizza?
The two fractions you need to look at are \( \frac{3}{6}\) and \( \frac{2}{6}\). Which has the bigger numerator?
The larger the numerator, the larger the fraction.
It can also help to draw each fraction to understand which one is larger.
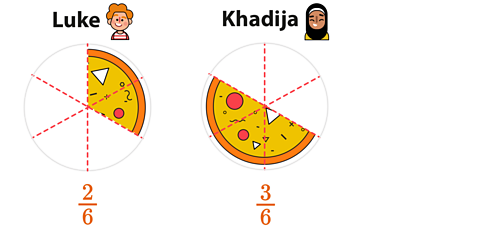
You can see that \( \frac{3}{6}\) is larger than \( \frac{2}{6}\), so Khadija ate more pizza!
Using the greater than and less than signs, you would write it as:
\( \frac{3}{6} > \frac{2}{6} \)
Watch: Bigger and smaller fractions
Finally, watch this clip from the Super Movers - Live Lesson all about working out which fractions are bigger and smaller. Why not play along at home?
Activity
Quiz
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count19 of 26

- count20 of 26

- count21 of 26

- count22 of 26
