Key points

ratioA part-to-part comparison. problems take different forms, which may include:
linking ratios and fractionThe result of one integer divided by another. It is written with one integer above the other with a horizontal line between them. The denominator must not be 0
part-part problems - where the value of one part of the ratio is given and the value of another ratio part has to be found
part-whole problems - where the value of one part of the ratio is given and the value of the whole has to be found
comparison problems - where the ratio and the difference between the values is given
problems where values change, giving a new ratio
In order to solve ratio problems, an understanding of the structure of the problem is needed. A bar modelOne or more rectangular bars drawn to represent information. may help to clarify this.
An understanding of equivalent ratios and simplifying ratios, as well as division in a given ratio is needed to solve ratio problems.

Solving problems involving ratios and fractions
To solve a problem involving ratios and fractions, you may be given the ratioA part-to-part comparison. or the fractionThe result of one integer divided by another. It is written with one integer above the other with a horizontal line between them. The denominator must not be 0.
When given the ratio:
Add the ratio parts together to find the denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1тБД3, the denominator is 3 of the fraction.
The numeratorNumber written at the top of a fraction. The numerator is the number of parts used. Eg, for 1тБД3, the numerator is 1 of the fraction is the ratio part that is the focus of the question.
When given the fraction:
- The numerator of the fraction gives one of the ratio parts.
- Find the other ratio part by subtracting the numerator from the denominator.
- Write the ratio in the correct order.
Examples

Image caption, The ratio of horses to donkeys at an animal sanctuary is 5 : 2. What fraction of the animals are donkeys?
Image caption, Add the ratio parts (5 and 2) to find the denominator of the fraction. 5 + 2 = 7. The denominator is 7
Image caption, The numerator of the fraction is the ratio part that is the focus of the question (donkeys). The numerator is 2. The fraction of the animals that are donkeys is 2тБД7
Image caption, To make pink paint, 2тБД5 red paint is mixed with white paint. How much white paint is needed? What is the ratio of red to white paint?
Image caption, The numerator of the fraction of red paint is 2. This is the ratio part for red paint. To find the ratio part for the white paint, subtract the numerator from the denominator. 5 тАУ 2 = 3. The ratio part for white paint is 3. 3тБД5 of the paint is white. The ratio of red to white paint is 2 : 3
1 of 5
Question
A farm has sheep and goats in the ratio 7 : 5 (sheep : goats). What fraction of the animals are sheep?
Add the ratio parts (7 and 5) to find the denominator of the fraction.
7 + 5 = 12. The denominator is 12
The numerator of the fraction is the ratio part that is the focus of the question (sheep). The numerator is 7
The fraction of animals that are sheep is \( \frac{7}{12} \)

Solving part-part and part-whole ratio problems
A part-part ratio problem is where the value of one part of the ratio is given and the value of another ratio part has to be found. A part-whole problem is where the value of one part of the ratio is given and the value of the whole has to be found.
Given a ratio and the value of one part of the ratio, find the value of another ratio part or the value of the whole.
Draw a bar modelOne or more rectangular bars drawn to represent information. split into the total number of parts. Label with the given information to represent the problem.
Find the value of one part by dividing the given value by the associated number of parts.
To find the value of another ratio part in a part-part problem, multiply the value of one part by the number of parts asked for.
To find the whole in a part-whole problem, multiply the value of one part by the total number of parts.
Examples
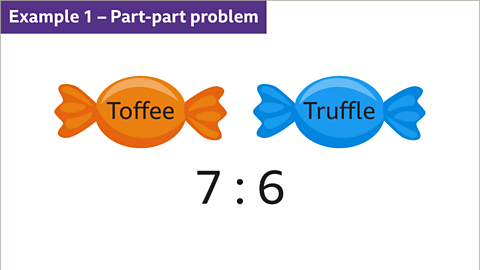
Image caption, A box contains toffees and truffles in the ratio 7 : 6. There are 24 truffles. How many toffees are there?
Image caption, Draw a bar model and label it to illustrate the problem. The ratio of toffees to truffles is 7 : 6. Draw 7 parts for the toffees and 6 for the truffles. Label the truffle bar with 24. To work out the total number of toffees, the value of one part needs to be found.
Image caption, To work the value of one part, divide the number of truffles (24) by the number of parts given (6). This gives the value of one part. 24 ├╖ 6 = 4
Image caption, Multiply the value of one part (4) by the number of parts asked for: the toffees (7). 4 ├Ч 7 = 28. There are 28 toffees in the box.
Image caption, A library stocks books for children and books for adults in the ratio 3 : 5. There are 450 books for children. How many books are in the library?
Image caption, Draw a bar model and label it to illustrate the problem. The ratio of books for children to books for adults is 3 : 5. Draw 3 parts for books for children and 5 parts for books for adults. Label the books for children bar with 450. To work out the total number of books, the value of one part needs to be found.
Image caption, To find the value of one part, divide the amount of books for children (450) by the number of parts given (3). 450 ├╖ 3 = 150. The value of one part is 150
Image caption, Multiply the value of one part (150) by the number of parts asked for: the number of books in the library. This is the total of books for children parts and the books for adults parts. (3 + 5 = 8). The calculation is 150 ├Ч 8. The total number of books in the library is 1200.
1 of 8
Question
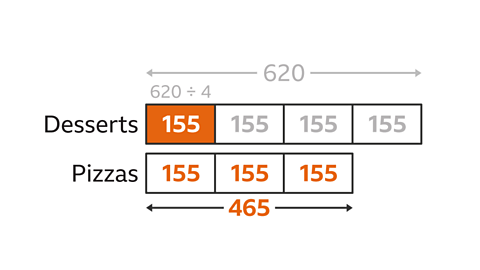
The ratio of desserts to pizzas in a supermarket freezer is 4 : 3
There are a total of 620 desserts.
How many pizzas are in the freezer?
Draw a bar model to illustrate the problem. The ratio of desserts to pizzas is 4 : 3. Draw 4 parts for desserts and 3 parts for pizzas.
Label it to illustrate the problem. Label the dessert bar with 620. To find the number of pizzas in the freezer, work out the value of one part.
To find the value of one part, divide the share for desserts (620) by the number of parts (4). 620 ├╖ 4 = 155. The value of one part is 155
Multiply the value of one part (155) by the number of parts asked for: pizzas (3). 155 x 3 = 465
The number of pizzas in the freezer is 465
Solving ratio problems involving comparisons
Some ratio problems involve a comparison between values. The comparison is the value difference between two parts of the ratio.
Given a ratio and a comparison between values:
Draw a bar model to illustrate the problem.
Label the given information.
Find the value of one part by dividing the comparison value by the number of parts given.
Multiply the value of one part by the number of parts of the object of the question.
Examples

Image caption, Everyone at a fancy dress party is dressed up as either a vampire or a wizard. The ratio of people dressed as vampires to wizards is 5 : 2. If there are 6 more vampires than wizards, how many people are at the party?
Image caption, Draw a bar model to illustrate the problem. The ratio of vampires to wizards is 5 : 2. There are 5 parts for the vampires and 2 parts for the wizards.
Image caption, Label the given information. There are 6 more vampires than wizards. The diagram shows the comparison between the vampires bar and the wizards bar. To work out the total number of people at the party, the value of one part needs to be found.
Image caption, To find the value of one part, divide the difference value (6) by the number of parts that make up the difference (3). 6 ├╖ 3 = 2. The value of one part is 2
Image caption, Multiply the value of one part (2) by the number of parts asked for (all the people so all the parts, 7). 2 ├Ч 7 = 14. The total number of people at the party is 14
Image caption, The ratio of the number of tulips to daffodils in a flower display is 3 : 7. There are 96 fewer tulips than daffodils. Find the number of daffodils in the display.
Image caption, Draw a bar model to illustrate the problem. The ratio of tulips to daffodils is 3 : 7. There are 3 parts for tulips and 7 parts for daffodils.
Image caption, Label the given information. There are 96 fewer tulips than daffodils. The diagram shoes the comparison between the tulips bar and the daffodils bar. To work out the number of daffodils in the display, the value of one part needs to be found.
Image caption, To find the value of one part, divide the comparison value (96) by the number of parts that make up the difference (4). 96 ├╖ 4 = 24. The value of one part is 24
Image caption, Multiply the value of one part (24) by the number of parts asked for (all the daffodils, 7 parts). 24 ├Ч 7 = 168. The number of daffodils in the display is 168
1 of 10
Question
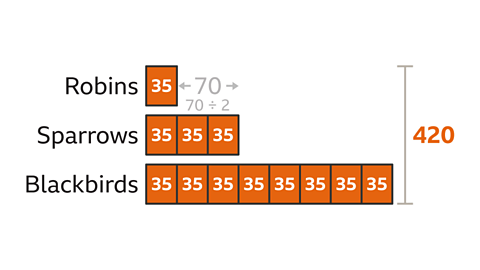
The ratio of the number of robins to sparrows to blackbirds in a survey of garden birds is 1 : 3 : 8 (robins : sparrows : blackbirds)
There were 70 fewer robins than sparrows. How many birds were observed in this survey?
Draw a bar model to illustrate the problem. The ratio of robins to sparrows to blackbirds is 1 : 3 : 8. There is 1 part for robins, 3 for sparrows and 8 for blackbirds.
Label the given information. There are 70 fewer robins than sparrows. This is the difference between the robins bar and the sparrows bar. To find the total number of birds in the survey, the value of one part needs to be found.
To find the value of one part, divide the difference value (70) by the number of parts that make up the difference (2). 70 ├╖ 2 = 35. The value of one part is 35
Multiply the value of one part (35) by the number of parts asked for (all the parts, 12). 35 x 12 = 420
Solving ratio problems with changing amounts
Given a ratio and total amount, find the new changing amounts and find the new ratio:
A total amount and ratio is given. Draw a bar model to illustrate this starting information.
Divide the total amount in the initial ratio.
- Find the value of one part by dividing the total amount by the sum of the parts.
- Multiply the value of one part by the number of parts for each share of the ratio.
Adjust the shared amounts according to the given information in the question.
Write the new amounts as a ratio and simplify, if necessary, by dividing the parts by their highest common factor (HCF) The largest factor that will divide into the selected numbers. Eg, 10 is the highest common factor of 30 and 20. Highest common factor is written as HCF. (HCF).
In this example, you need to be able to divide in a given ratio and simplify ratios.
Example

Image caption, A market stall has 60 T-shirts. The ratio of small, medium and large T-shirts being sold on the stall is 2 : 3 : 1. The stallholder sells 26 medium and 2 large T-shirts. What is the ratio of small, medium and large T-shirts now?
Image caption, Draw a bar model to illustrate the starting information. Draw 2 parts for small T-shirts, 3 for medium and 1 for large. The total number of T-shirts is 60
Image caption, Divide 60 in the ratio 2 : 3 : 1. To find the value of one part, divide the total number (60) by the sum of the parts (2 + 3 + 1 = 6). 60 ├╖ 6 = 10. The value of one part is 10
Image caption, 2 parts are small, so 2 ├Ч 10 = 20 small T-shirts. 3 parts are medium, so 3 ├Ч 10 = 30 medium T-shirts. 1 part is large, so 1 ├Ч 10 = 10 large T-shirts.
Image caption, Adjust the shared amounts according to the given information in the question. At the start there were 20 small, 30 medium and 10 large T-shirts. 26 medium and 2 large T-shirts are sold. The remaining T-shirts are 20 small, 4 medium and 8 large T-shirts.
Image caption, The ratio of small to medium to large T-shirts is now 20 : 4 : 8. This ratio can be simplified.
Image caption, To simplify the ratio, divide each part by their highest common factor (HCF). The HCF of 20, 4 and 8 is 4. Divide each part by 4. The new simplified ratio of small to medium to large T-shirts is 5 : 1 : 2
1 of 7
Question
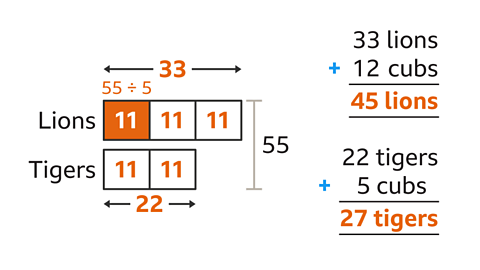
There are 55 big cats in a safari park.
The ratio of lions to tigers is 3 : 2
12 lion cubs and 5 tiger cubs are born. What is the ratio of lions to tigers now?
A total amount and ratio is given. Draw a bar model to illustrate this starting information. Draw 3 parts for lions and 2 parts for tigers, with a total of 55
Divide the total number of big cats (55) in the ratio 3 : 2. To find the value of one part, divide the amount (55) by the total number of parts (5). 55 ├╖ 5 = 11. The value of one part is 11. Multiply one part by the number of parts for each big cat. There are 11 ├Ч 3 = 33 lions. There are 11 ├Ч 2 = 22 tigers.
Adjust the shared amounts according to given information in the question. After the cubs have been born there are 33 + 12 = 45 lions and 22 + 5 = 27 tigers.
Write the new shares as a ratio and simplify. The new ratio of lions to tigers is 45 : 27. This ratio can be simplified by finding the HCF of 45 and 27. This is 9. Divide each ratio share by 9. The ratio simplifies to 5 : 3
The ratio of lions to tigers is now 5 : 3
Practise solving ratio problems
Quiz
Practise solving ratio problems in this quiz. You may need a pen and paper to complete these questions.
Real-world maths

Ratio problems occur in many different contexts.
Successful cookery relies on the ratio of the ingredients used. For example:
To make meringues, you need a ratio of 2 parts sugar to 1 part egg white.
To make Yorkshire puddings, you need equal amounts of egg, flour and milk (and a pinch of salt). The ratio of egg, flour and milk is 1 : 1 : 1
In construction, fencing companies use a fixed ratio of concrete mix to water to secure fence posts. For a given amount of concrete mix, the amount of water needed is worked out. This is a part-to-part ratio problem.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from │╔╚╦┬█╠│ Bitesize.

More on Ratio
Find out more by working through a topic
- count4 of 5

- count5 of 5
- count1 of 5
- count2 of 5