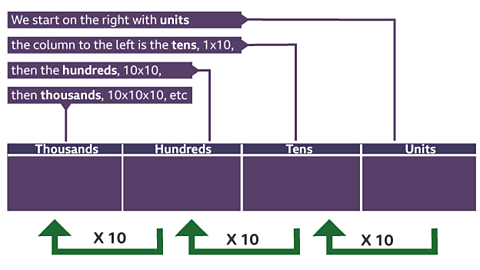
Before reading this guide, it may be helpful to read the guides from Module 1 (M1) on decimals and M2 Rounding to significant figures.
Trial and improvement
Trial and improvement is a method for solving equations when there is no exact answer.
You may also be asked to give the solution to a given number of decimal places or significant figures. The question will usually indicate the degree of accuracy required.
When solving an equation by trial and improvement:
- Choose a sensible 'starting value'.
- Substitute this value into the left hand side (LHS) of the equation
- Use a calculator to evaluate it
- Decide whether the value obtained is too big or too small
- Choose an improved value and re-evaluate
- Repeat steps 2–5 until the answer and the previous one round to the given accuracy
This process is usually recorded on a table.
Example
Using trial and improvement, solve the equation \(x^{3} + x = 20\)
Give your answer correct to one decimal place.
Solution
First, choose a starting value.
\(x = 3\) is clearly too big as \(x^{3}\) is 27 and the target value is 20.
\(x = 2\) is a sensible starting value
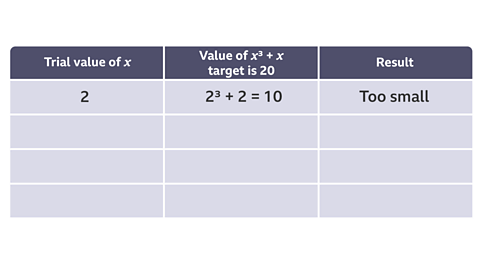
Image caption, The result is too small so choose a larger value. Try 2.5
Image caption, The result is getting closer but is still too small. Try 2.6
Image caption, The result is now too big. X must lie between 2.5 and 2.6. Try 2.55, which is halfway between 2.5 and 2.6.
Image caption, 2.6 is too big and 2.55 is too small so the answer must lie in between these two values.
1 of 4
Any value inbetween 2.55 and 2.6 will round to 2.6.
Answer
\(x = 2.6\) (correct to one decimal place).
To get all of the marks, you must show all the steps.
Question
The table below shows the start of a trial and improvement method to solve the equation \(2x^{3} – x = 40\).
Continue the process and give your answer to one decimal place.
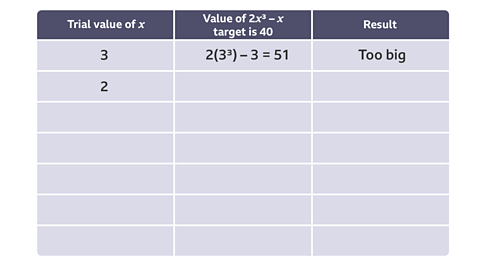

The solution is bigger than 2.75 but smaller than 2.8. Any number in this range will round to 2.8 to one decimal place.
Answer
\(x = 2.8\) (to 1 d.p.)
Question
Using trial and improvement, solve the equation \(x^{4} – x – 140 = 0\).
Give your answer correct to two decimal places.
First, rearrange the equation so that the terms in x are all on the left-hand side of the equation.
- \(x^{4} – x = 140\)
Then, set up a table.

Solution is between 3.46 and 3.465. Any number in this range will round to 3.46.
Answer
\(x = 3.46\) to 2 decimal places.
Question
Use trial and improvement to find a solution of the equation \(x^{3} + 2x = 22\).
Give your answer correct to 2 decimal places. You must show all your working.
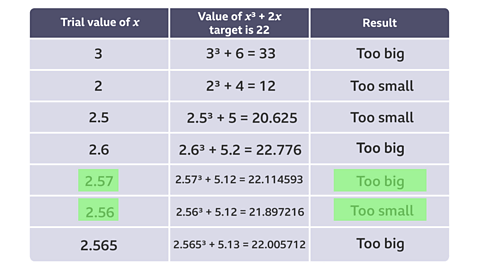
The solution is between 2.56 and 2.565. Any number in this range will round to 2.56 to 2 decimal places.
Answer
\(x = 2.56\) to 2 d.p.
Test yourself
Question 1
Use trial and improvement to find a solution to the equation \(x^2 + \frac {x}{2} = 17\)Give your answer correct to 1 decimal place.
You should show all your working in exam conditions
Solution:
| Trial value of x | Value of \(x^2 + \frac{x}{2}\) Target is 17 | Result |
|---|---|---|
| 3 | \(3^2 + \frac{3}{2} = 10.5\) | Too small |
| 4 | \(4^2 + \frac{4}{2} = 18\) | Too big |
| 3.5 | \(3.5^2 + \frac{3.5}{2} = 14\) | Too small |
| 3.6 | \(3.6^2 + \frac{3.6}{2} = 14.76\) | Too small |
| 3.7 | \(3.7^2 + \frac{3.6}{2} = 15.54\) | Too small |
| 3.8 | \(3.8^2 + \frac{3.8}{2} = 16.34\) | Too small |
| 3.9 | \(3.9^2 + \frac{3.9}{2} = 17.16\) | Too big |
| 3.85 | \(3.85^2 + \frac{3.85}{2} = 16.7475\) | Too small |
The solution is between 3.85 and 3.9. Any number in this range rounds to 3.9
Answer x = 3.9 to 1 d.p.
Question 2
Use trial and improvement to find a solution to the equation \(\frac{x^2}{2}\ +\ x\ = 35\)
Give your answer correct to 1 decimal place
You should show all your working in exam conditions
Solution:
| Trial value of x | Value of \(\ \frac{x^2}{2}\ +\ x\) Target is 35 | Result |
|---|---|---|
| 8 | \(\frac{8^2}{2}\ +\ 8\ =\ 40\) | Too big |
| 7 | \(\frac{7^2}{2}\ +\ 7\ =\ 31.5\) | Too small |
| 7.5 | \(\frac{{7.5}^2}{2}\ +\ 7.5\ =\ 35.625\) | Too big |
| 7.4 | \(\frac{{7.4}^2}{2}\ +\ 7.4\ =\ 34.78\) | Too small |
| 7.45 | \(\frac{{7.45}^2}{2}\ +\ 7.45\ =\ 35.20125\) | Too big |
7.4 is too small and 7.45 is too big so the solution is somewhere in between.
Any number in this range will round to 7.4.
Answer x = 7.4 correct to 1 d.p.
More on M6: Algebra
Find out more by working through a topic
- count1 of 5