Before starting this guide, it may be helpful to read the guide from .
Key points
simultaneousHappening at the same time. equations are two or more equations that share variableAn unknown value, usually represented by a letter like ØÆÖ or ØÆÜ.
For example, \(y\) = 2\(x\) - 1 and \(y\) = \(x\) + 1 share the variables \(x\) and \(y\). They are simultaneous because the equations are solved at the same time.Simultaneous equations can be solved algebraically or graphically.
To solve simultaneous equations graphically, it is essential to be able to draw the graph of a straight line.

Representing equations graphically
Each equation is used to create a table of values, which are then plotted as coordinateThe ordered pair of numbers (ØÆÖ, ØÆÜ) that defines the position of a point. pairs on the same set of axesTwo reference lines, one horizontal and one vertical, that cross at right-angles. They are used to define the position of a point on a grid. Axes is the plural of axis. .
Graphs are often written in the form \(y\) = \(mx\) + \(c\), where \(m\) is the gradientA measure of the slope of a line. The steeper the line, the greater the gradient. The gradient is represented by ØÆÄ in the equation ØÆÜ = ØÆÄØÆÖ + ØÆä (how steep the line is) and \(c\) is the \(y\)-ØÆÜ-Š▒▓į│┘▒░∙│”▒▒Ķ│┘The point at which the line crosses the ØÆÜ-axis. Commonly referred to as ŌĆśthe interceptŌĆÖ..
If the two lines cross, then the coordinates of this intersectWhere lines cross or overlap. are the solutions to the simultaneous equations. If the lines are parallel (and therefore do not intersect), there is no solution.
Example
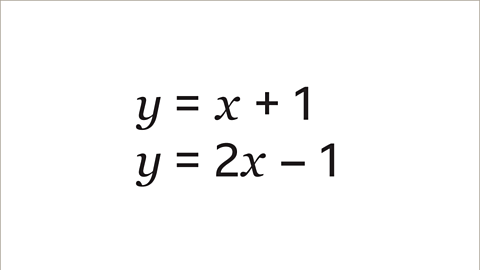
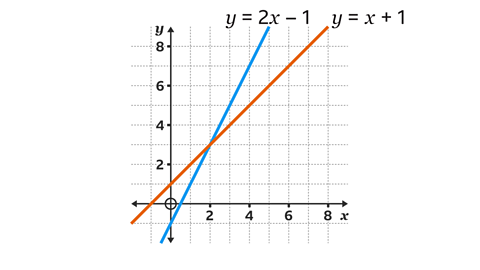
Image caption, Use the graphical method to solve the simultaneous equations.
Image caption, Both equations are in the form ØÆÜ = ØÆÄØÆÖ + ØÆä. For the equation ØÆÜ = ØÆÖ + 1, the gradient (ØÆÄ) is 1 and the intercept (ØÆä) is +1. For the equation ØÆÜ = 2ØÆÖ ŌĆō 1, the gradient (ØÆÄ) is 2 and the intercept (ØÆä) is -1
Image caption, To solve the equations graphically, the two lines ØÆÜ = ØÆÖ + 1 and ØÆÜ = 2ØÆÖ - 1 are drawn on the same diagram. The coordinates of the point of intersection of the two graphs are the solutions to the simultaneous equations. Draw a table of values for the graph ØÆÜ = ØÆÖ + 1. A minimum of three pairs of values are required. When ØÆÖ = 0 then ØÆÜ = 1 (0 + 1 = 1). When ØÆÖ = 1 then ØÆÜ = 2 (1 + 1 = 2). When ØÆÖ = 2 then ØÆÜ = 3 (2 + 1 = 3).
Image caption, Draw a table of values for the graph ØÆÜ = 2ØÆÖ - 1. A minimum of three pairs of values are required. When ØÆÖ = 0 then ØÆÜ = -1 (2 x 0 - 1 = -1). When ØÆÖ = 1 then ØÆÜ = 1 (2 x 1 - 1 = 1). When ØÆÖ = 2 then ØÆÜ = 3 (2 x 2 - 1 = 3).
Image caption, Plot the three coordinate pairs from the table onto the axes. Extend the line. This is the graph for the equation ØÆÜ = ØÆÖ + 1
Image caption, Plot the three coordinate pairs from the table onto the axes. Extend the line. This is the graph for the equation y = 2ØÆÖ - 1
Image caption, Draw both graphs on the same set of axes. Label each line with the correct equation.
Image caption, The two lines intersect with each other. This means there is a solution. The lines intersect at the point (2, 3). The solution to the simultaneous equations is ØÆÖ = 2 and ØÆÜ = 3
1 of 8
Question
What is the solution to the pair of equations \(y\) = \(x\) + 3 and \(y\) = 2\(x\) + 1?
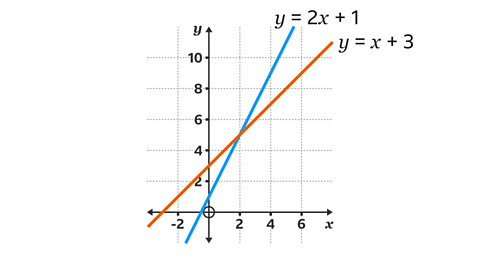

The two equations have been drawn as linear graphs.
The point of intersection is (2, 5)
The solution to the pair of equations is \(x\) = 2 and \(y\) = 5
Rearranging equations to solve problems
To be able to solve simultaneous equations, both equations need to be in the form \(y\) = \(mx\) + \(c\)
If the equations are not in the form \(y\) = \(mx\) + \(c\), the equations need to be rearranged.
Example
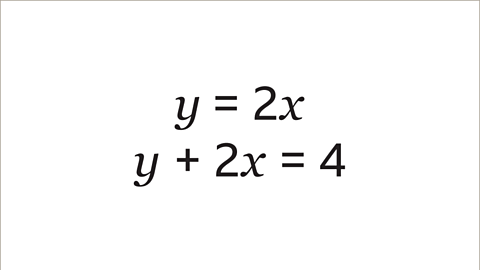
Image caption, Use the graphical method to solve the simultaneous equations.
Image caption, The two equations need to be in the form ØÆÜ = ØÆÄØÆÖ + ØÆä. The equation ØÆÜ = 2ØÆÖ is written in this form. However, ØÆÜ + 2ØÆÖ = 4 is not and needs to be rearranged.
Image caption, Rearrange the second equation. The two equations are now ØÆÜ = 2ØÆÖ and ØÆÜ = -2ØÆÖ + 4. Each of these two equations is in the form ØÆÜ = ØÆÄØÆÖ + ØÆä and can be plotted as a straight-line graph.
Image caption, This graph shows ØÆÜ = 2ØÆÖ. The straight line shows the different values of ØÆÖ and ØÆÜ that follow the rule. For example, for the point (1, 2), the ØÆÖ coordinate is 1 and the ØÆÜ coordinate is 2. The point (2, 4) is another pair of values that follows the same rule. The ØÆÖ-coordinate is 2 and the ØÆÜ-coordinate is 4
Image caption, This graph shows ØÆÜ = -2ØÆÖ + 4. The straight line shows the different values of ØÆÖ and ØÆÜ that follow the rule. For example, for the point (2, 0), the ØÆÖ-coordinate is 2 and the ØÆÜ-coordinate is 0. There are lots of other pairs of points on the graph that also follow the rule.
Image caption, To solve the simultaneous equations draw both graphs on the same axes.
Image caption, The two lines cross at the point (1, 2). This is called the point of intersection. The values of ØÆÖ and ØÆÜ at this single point are the solutions of the simultaneous equations. The solution to the equations ØÆÜ = 2ØÆÖ and ØÆÜ + 2ØÆÖ = 4 is ØÆÖ = 1 and ØÆÜ = 2
1 of 7
Question
What is the solution to the pair of equations \(y\) = \(x\) + 5 and \(y\) = 7 ŌłÆ \(x\)?
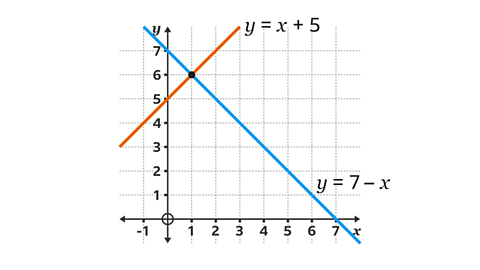
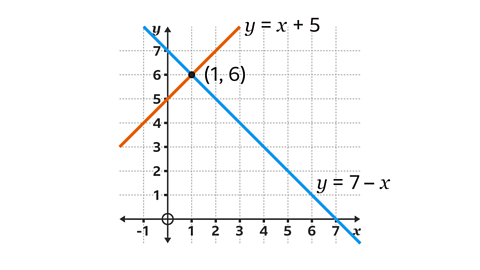
The two equations have been drawn as linear graphs.
The point of intersection is (1, 6).
The solution to the pair of equations is \(x\) = 1 and \(y\) = 6
Real-life maths

A company will use graphs of simultaneous equations to model the potential profits it can make by selling its products at a different price. The company will have fixed costs and variableA quantity that can take on a range of values. costs, depending on how much of something it produces.
revenueThe money a company earns from the sale of its products and services. will be made by multiplying the sale price by the number of units sold. Where the two lines on the graph intersect will be the ŌĆśbreak-evenŌĆÖ point (the number of sales needed before the company begins to make a profit). Using a spreadsheet, the company can make financial decisions, including the profits they might make or the effect of lowering (or raising) the price of what it sells.

Test yourself
More on M6: Algebra
Find out more by working through a topic
- count1 of 5