A straight line can be drawn by joining two points plotted on a grid.
The coordinates of the mid-point of the line and the length of the line can be calculated using the coordinate values.
Before you start, it may be helpful to read the guide on coordinates and graphs from M1 and the guide on Pythagoras' theorem from M2.
Midpoint of a line
To find the midpoint of a line between two sets of coordinates, find the average of the \(x\)-axis coordinates and the average of the \(y\)-axis coordinates.
Example
Find the midpoint of the line joining the point D \((10, 5)\) and E \((4, 11)\).
Average of \(x\)-coordinates ŌĆā ŌĆā ŌĆā \(\frac{10+4}{2}=7\)
Average of \(y\)-coordinates ŌĆā ŌĆā ŌĆā \(\frac{5+11}{2}=8\)
The midpoint is \((7, 8)\).
It may be helpful to set out your work like this:

Question
A is the point \((ŌĆō7, 4)\) and B is the point \((5, ŌĆō8)\). M is the midpoint of the line AB.
What are the coordinates of M?

Example
P is the point with coordinates \((ŌĆō5, 5)\) and Q is the point with coordinates \((x, y)\).
M is the midpoint of PQ and has coordinates \((ŌĆō1, 3)\).
Find the coordinates of Q.
Solution
In this question, the midpoint is known and one of the end points has to be found.
Use \((x, y)\) for the coordinates of Q and apply the same method as before.
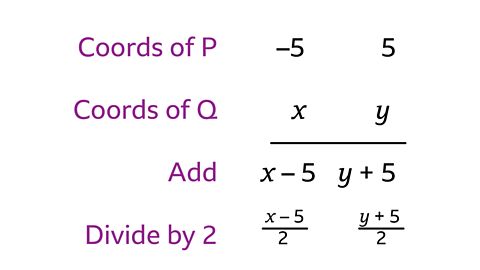
Set up an equation using \(x\)-coordinates \(\frac{xŌĆō5}{2}ŌĆō1\) M is the point \((ŌĆō1, 3)\)
Solve equation
- Multiply across by 2 ░└(│µŌĆō5=ŌĆō2░└)
- Add 5 to each side ░└(│µŌĆō5+5=ŌĆō2+5░└)
\(x=3\)
Set up an equation using \(y\)-coordinates
\(\frac{5+y}{2}=3\)M is the point \((ŌĆō1, 3)\)
Solve equation \(5+y=6\)
\(y=1\)
Coordinates of Q are \((3,1)\)
Answer
The coordinates of Q are \((3,1)\)
Question
M is the midpoint of a line joining points J and K.
J is the point \((2, ŌĆō3)\) and M is the point \((5, 1)\).
What are the coordinates of K?
Answer
Let the coordinates of K be \((x, y)\)

Equation using \(x\)-coordinates:
ŌĆāŌČ─āŌČ─āŌČ─āŌČ─āŌČ─ā\(░└┤┌░∙▓╣│”Ą„│µ+2░©Ą„2░©=5░└)
ŌĆāŌČ─āŌČ─āŌČ─āŌČ─āŌČ─ā\(│µ+2=10░└)
ŌĆāŌČ─āŌČ─āŌČ─āŌČ─āŌČ─ā\(│µ=8░└)
Equation using \(y\)-coordinates:
ŌĆāŌČ─āŌČ─āŌČ─āŌČ─āŌČ─ā\(░└┤┌░∙▓╣│”Ą„▓ŌŌĆō3░©Ą„2░©=1░└)
ŌĆāŌČ─āŌČ─āŌČ─āŌČ─āŌČ─ā\(▓ŌŌĆō3=2░└)
ŌĆāŌČ─āŌČ─āŌČ─āŌČ─āŌČ─ā\(▓Ō=5░└)
Coordinates of K are \((8,5)\)
Length of a line
To find the length of a line between points
- Subtract the \(x\)-coordinates
- Subtract the \(y\)-coordinates
- Apply Pythagoras' theorem to these values
Example
Find the length of the line joining D \((6, 9)\) and E \((ŌĆō2, 3)\)
Solution
- Subtract the \(x\)-coordinates
░└(6ŌĆō2=6+2=8░└)
- Subtract the \(y\)-coordinates
░└(9ŌĆō3=6░└)
- Apply Pythagoras' theorem to these values
\(length=\sqrt{8^2+6^2}\)
\(=\sqrt{100}\)
\(=10\)
It will be helpful to set out your work like this:
\(\matrix{ & &~x & ~y \cr Coords~of~D & &~6 & ~9 \cr Coords~of~E & - & -2 & ~3 \cr Subtract & & \hline ~8 & ~6}\)
Pythagoras Length = \(\sqrt{8^2 + 6^2}\)ŌĆāŌĆāŌĆā = \(\sqrt{100}\)ŌĆāŌĆāŌĆā = \(10\)
Question
Find the length of the line by joining R \((11, 3)\) and S \((ŌĆō4, ŌĆō5)\).
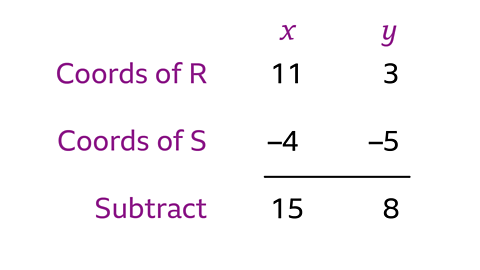
Applying Pythagoras' theorem:
\(length=\sqrt{15^2+8^2}\)
\(=\sqrt{289}\)
\(=17\)
The line is 17 units long.
Test yourself
More on M2: Algebra
Find out more by working through a topic
- count1 of 5
- count3 of 5
