PythagorasÔÇÖ Theorem
PythagorasÔÇÖ Theorem states that, in a right-angled triangle, the square of the longest side is equal to the sum of the squares of the other two sides.
a┬▓ + b┬▓ = c┬▓
Finding the length of the hypotenuse
To find the length of the hypotenuse when the lengths of two shorter sides are known:
- Substitute the known lengths into PythagorasÔÇÖ theorem
- Calculate the value of H┬▓ (H is Hypotenuse)
- Calculate H by finding the square root of H┬▓
Example
Find the length of the hypotenuse on this right-angled triangle.
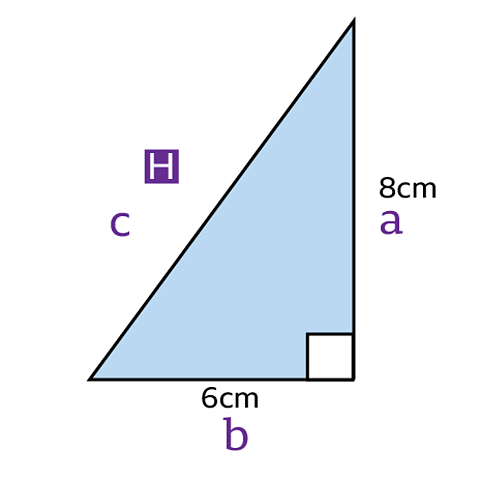
Substitute the known lengths into PythagorasÔÇÖ theorem
- \(a^2 + b^2 = c^2\)
- \(8^2 + 6^2 = H^2\)
Calculate the value of H┬▓
- \(64 + 36 = H^2\)
- \(H^2 = 100\)
Calculate H by finding the square root of H┬▓
- \(H = \sqrt{100} = 10cm\) .

Question
Find the length of the side marked x.

Solution
\(\mathbf {a^2 + b^2 = c^2}\)
\(22^2 + 25^2 = X^2\)
\(X^2 = 484 + 625 = 1109\)
\(X = \sqrt{1109} = 33.30165ÔÇŽ\)
Answer:
X = 33.3 mm (to 1 decimal place)
Question
Calculate the distance diagonally across a rectangular field measuring 18 m by 24 m.
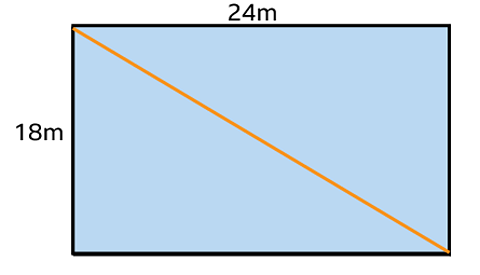
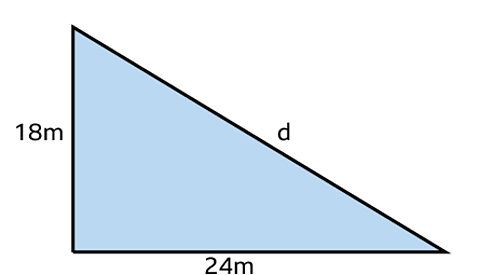
Then use PythagorasÔÇÖ theorem.
- \(d^2 = 18^2 + 24^2 = 900\)
- \(d = \sqrt{900} = 30\)
Answer:
The diagonal is 30 m
Finding the length of a shorter side
To find the length of a shorter side when the length of the hypotenuse and the other shorter side are known:
- Substitute the known lengths into PythagorasÔÇÖ theorem
- Calculate the value of the square of the missing side
- Find the square root of this value to get the length of the missing side.
Example
Find the height of a phone with a diagonal screen size of 17 cm and a width of 8 cm.

Substitute the known lengths into PythagorasÔÇÖ theorem
- \(17^2 = x^2 + 8^2\)
Calculate the value of the square of the missing side
- \(x^2 = 17^2 + 8^2 = 225\)
Find the square root of this value to get the length of the missing side.
- \(x = \sqrt{225} = 15\)
The height of the phone is 15 cm

Question
Calculate the perimeter of this triangle.
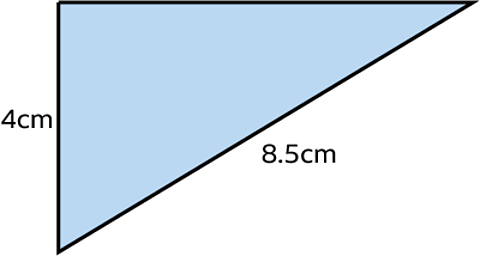
Solution
Remember: the perimeter is the total distance around the shape.
It is necessary to know the length of all 3 sides. The missing length can be calculated using PythagorasÔÇÖ theorem.
\(a^2 + b^2 = c^2\)
\(4^2 + b^2 = 8.5^2\)
\( b^2 = 8.5^2ÔÇô 4^2\)
\(b = \sqrt{56.25} = 7.5 cm\)
Perimeter = 4 + 7.5 + 8.5 = 20 cm
Deciding if a triangle has a right angle
If the three sides of a triangle are known PythagorasÔÇÖ theorem can be used to decide if the triangle is right-angled or not.
To do this
- Substitute the lengths of the sides into PythagorasÔÇÖ theorem
- If both sides of the equation are equal the triangle is right-angled
- If both sides of the equation are not equal the triangle is not right-angled
Example
Does this triangle have a right angle?
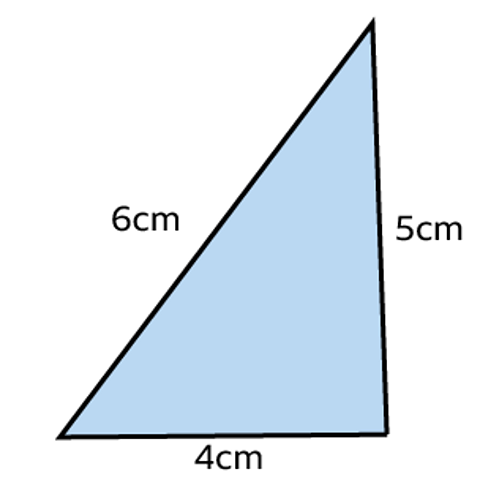
\(a^2 + b^2 = c^2\)
\(4^2 + 5^2 = 6^2\)
\(16 + 25 = 36\)
\(41 \neq 36\)

The two sides of the equation are not equal so the triangle does not have a right angle.
Example
Does this triangle have a right angle?
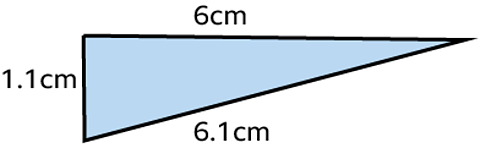
\(a^2 + b^2 = c^2\)
\(1.1^2 + 6^2 = 6.1^2\)
\(1.21 + 36 = 37.21\)
\(37.21 = 37.21\)
The two sides of the equation are equal so the triangle has a right angle.
Question
Is this a right-angled triangle?
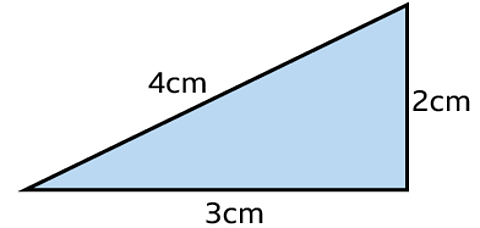
Solution
\(a^2 + b^2 = c^2\)
\(2^2 + 3^2 = 4^2\)
\(4 + 9 = 16\)
\(13 \neq 16\)
The two sides of the equation are not equal so this is not a right-angled triangle.
Test yourself
More on M2: Geometry and measures
Find out more by working through a topic
- count4 of 4