Module 3 (M3) - Algebra - Factorising

Factorising quadratic expressions

Factorising an expression means finding the factors that multiply together to give that expression.

A quadratic expression is one that has an ‘��²’ term as its highest power.

\(\mathbf {x^2}\), \(\mathbf {2x^2 -3x}\), \(\mathbf {x^2 - 9}\) and \(\mathbf {x^2 + 5x + 6}\) are all quadratic expressions.

Some quadratic expressions cannot be factorised.

Factorising quadratic expressions of the form \(\mathbf {x^2 + bx + c}\)

To find a method for factorising an expression such as \(\mathbf {x^2 + 5x + 6}\), look at how that expression was arrived at by expanding two brackets.

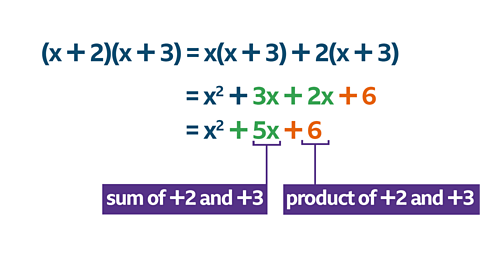
(x + 2)(x + 3) = x(x + 3) + 2(x + 3) = x2 + 3x + 2x + 6 = x2 + 5x + 6

There are three terms in the expanded expression:

First term:
��²

Second term:
sum of +2x and +3x

Third term:
product of +2 and +3

This information gives us a method for factorising.

Examples

Factorise \(\mathbf {x^2 + 2x – 15}\):

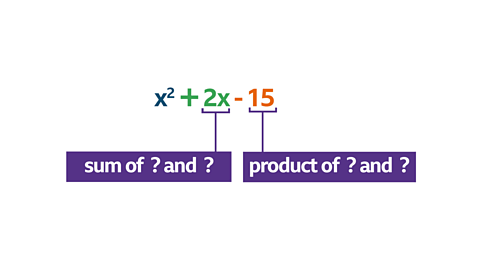
To Factorise:

Find two numbers whose sum is +2 and whose product is –15

The product is minus 15, so one of factors must be negative.

The numbers needed are either:

+5 and -3 or -5 and +3 As the sum is positive, the pair with the higher + value is the one to choose i.e.
+5 and -3

Write down the factors:

\(\mathbf {x^2 + 2x – 15 = (x + 5)(x – 3)}\)

Answer:
\(\mathbf {x^2 + 2x – 15 = (x + 5)(x – 3)}\)
\(\mathbf {(x - 3)(x + 5)}\) is also a correct answer. The order of the factors does not matter.

Question

Factorise \(��² + 5x – 24\)

Example

Factorise ��² - 9x + 20

Solution

Identify the product and sum of the two key values that we need to find.

Product = +20
Sum = - 9
- -4 and -5 add to give -9 and multiply to give +20
The factors are (x - 4) and (x - 5)

Answer: ��² - 9x + 20 = (x - 4)(x - 5)

Question

Factorise ��² - 17x + 70

Factorising expressions of the form ��²-a² (difference of two squares)

Expressions such as ��²-a² can be factorised using the difference of two squares method.

To understand how this works, look at the result when (x + 5)(x – 5) is expanded.

(x + 5)(x – 5) = x(x -5) + 5(x – 5) = ��² – 5x + 5x – 25 Since = ��²– 25 Expanding (x + 5)(x – 5) gives ��² – 25

The inverse of this means that ��² – 25 factorises to give (x + 5)(x – 5)

Note that in the expression ��² – 25 x is squared
25 = 5² and there is a minus sign in between so we have the difference of two squares!

In general, ��² – a² can be factorised to give (x + a)(x – a)

Both ��² and 100 (10²) are squares and there is a - sign in between.

Use the difference of two squares method - DOTS.

The factors can be written down without any further working.

��² – 100 = ��² – 10²

= (x + 10)(x – 10)

Question

Factorise ��² - 49

Example

Factorise 9 - ��²

DOTS can still be used here – the expression does not have to start with ‘��²”

9 - ��² = 3² - ��²

Factors are (3 + x)(3 – x)

Answer:
9 - ��² = (3 + x)(3 – x)

Difference of two squares (DOTS) often appears on exams

��̳