This builds on work you should already have covered in M2 Coordinates and Graphs
A straight line drawn on a grid can be described by a rule connecting the x and y coordinates of every point on the line.
This is known as the equation of the line.
General form of the equation of a line
The equation of any straight line can be written in the form \(y = mx + c\) where \(m\) and \(c\) are numbers and \(x\) and \(y\) represent the \(x\) and \(y\) coordinates.
The equation is a rule connecting the \(x\) and \(y\) coordinates - the rule is true for all points on the line.
For example:
For the line \(y = 2x -3\), for any value of \(x\) , the \(y\) coordinate can be found by doubling that value and subtracting 3.
Example
A line has the equation \(y = 5x + 2\). What are the coordinates of a point, P, on the line where \(x =-2\)?
Answer:
When \(x = -2\), \(y = 5(-2) + 2\)
\(=-8\)
Answer:
P is the point (-2, -8)
Question
Show that the point (5, -7) lies on the line \(y = -2x + 3\)?
Solution:
If (5, -7) is on the line, when x = 5, y should = -7.
\(y = -2x + 3\)
When \(x = 5, y = -2(5) + 3\)
\(= - 10 + 3\)
\(= -7\)
Answer
The point (5, -7) is on the line.
Gradient and intercept
When the equation of a straight line is in the form \(y = mx + c\), \(m\) and \(c\) are numbers which give useful information about the graph of the line.
Gradient
In the equation \(y = mx + c\), \(m\) is the gradient of the line. The gradient is a measure of how steep the line is.
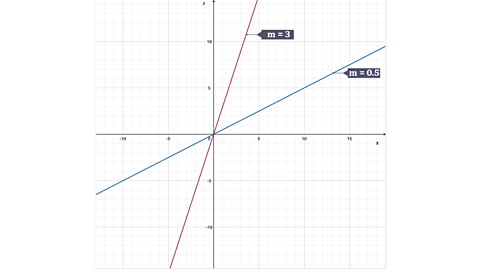
Image caption, The larger the value of m, the steeper the line
Image caption, A line which slopes from bottom left to top right has a positive gradient. A line which slopes from top left to bottom right has a negative gradient
Image caption, Parallel lines have the same gradient
1 of 3
Gradient from a graph
The gradient of a line can be found from its graph.
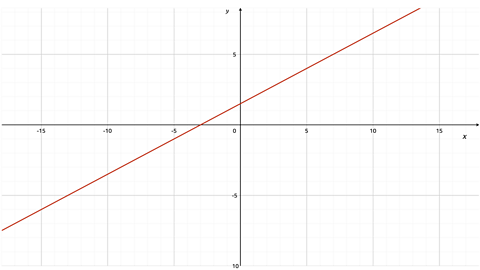
Image caption, Find the gradient of this line
Image caption, Choose two points on the line and complete a right angled triangle.
Image caption, Count the squares the two sides of the triangle
Image caption, Calculate gradient
Gradient = = 0.5
The gradient is 0.5
1 of 4
Gradient of a line joining two points
To find the gradient of a line joining two points, divide the difference in the y-coordinates by the difference in the x-coordinates.
This is sometimes given as an equation:
For points \((x_1, y_1)\) and \((x_2, y_2)\)
Gradient = \(\frac{y_2 - y_1}{x_2 - x_1}\)
Example:
Find the gradient of the line joining the point D (4, 11) and E (10, 5)
Solution
Difference in y-coordinates \( 11 - 5 = 6\)
Difference in x-coordinates \( 4 - 10 = -6\)
Gradient =\(\frac{difference~in~y~values}{difference~in~x~values} = \frac{6}{-6} = -1\)
It may be helpful to set out your work like this:
\(\matrix{ & ~x & ~y \cr Coordinates~of~D & ~4 & ~11 \cr Coordinates~of~E &10 & 5 \cr Subtract & \hline ~-6 & ~6}\)
Gradient =\(\frac{difference~in~y~values}{difference~in~x~values} = \frac{6}{-6} = -1\)
Alternatively, using the formula:
Gradient =\(\frac{y_2 - y_1}{x_2-x_1} = \frac{11-5}{4-10} = \frac{6}{-6} = -1\)
Question
J is the point (4, 5) and K is the point (7, -1).
What is the gradient of the line JK?
Solution:
\(\matrix{ & ~x & ~y \cr Coordinates~of~J & ~4 & ~5 \cr Coordinates~of~K & ~7 & -1 \cr Subtract & \hline -3 & ~6}\)
Gradient =\(\frac{difference~in~y~values}{difference~in~x~values} = \frac{6}{-3} = -2\)
Intercept
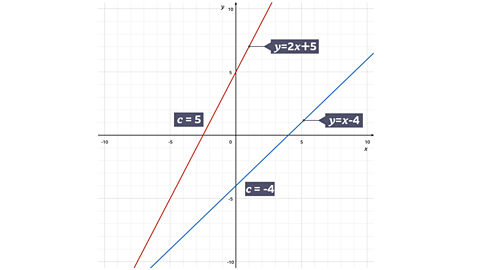
If a straight line does not go through the origin, it will cross the y axis at another point.
The y coordinate at the point where it crosses the y axis is called the intercept.
In the equation y = mx + c, c is the intercept.
Finding the equation of a line
If the coordinates of two points on a line are known, the equation of the line can be found by letting the equation be \(y = mx + c\) and then finding values for m and c.
If the value of either m or c is already known, the equation can be found using the coordinates of one point on the line.
If the gradient is known or has been calculated, a formula can be used.For points \((x_1, y_1)\) and \((x_2, y_2)\), this is:
\(y - y_1 = m(x - x_1)\)
Example
The equation of a line is \(2y + 3x = 8\)
- What is the gradient of the line?
- At what point does the line cross the y-axis?
Solution:
To determine the values of m and c, the line has to be in the form \(y = mx + c\).
Rearrange the equation
\(2y + 3x = 8\)
\(2y = -3x + 8\)
\(y = -\frac{3}{2}x + 4\)
The values for m and c can now be read from the equation
\(m = -\frac{3}{2}\) and \(c = 4\)
- The gradient of the line is \(m = -\frac{3}{2}\)
- The intercept is the point (0, 4)
Example
A straight line has a gradient of -2 and goes through the point P with coordinates (-3, 2).
What is the equation of the line?
Solution:
Let the equation of the line be \(y = mx + c\)
The gradient is -2
Put this value for m into the equation
\(y = -2x + c\)
To find the value for c, use the x and y coordinates of the point P, (-3, 2)
Substituting \(x = -3\) and \(y =2\) into the equation \(y = -2x + c\)
\(2 = -2(-3) + c\)
\(2 = 6 + c\)
\(c = -4\)
The equation of the line is y = -2x -4
Alternatively, using the formula:
\(y - y_1 = m(x - x_1)\)
Equation of the line is:
\(y - 2 = -2(x - (-3))\)
\(y - 2 = -2(x + 3)\)
\(y - 2 = -2x - 6\)
\(\mathbf{y = -2x - 4}\)
Question
A line crosses the y axis at the point (0, -1) and goes through the point (2, -11).
What is the equation of this line?
Hint - Let the equation be \(y = mx + c\) and find values for c and m
Solution:
Let the equation be \(y = mx + c\)
The line crosses the y axis at the point (0, -1) so c = -1
To find m
\(\matrix{ & ~x & ~y \cr & ~2 & -11 \cr & 0 & -1 \cr Subtract & \hline ~2 & -10}\)
Gradient = \(\frac{-10}{2} = -5\)
Equation of line is \(\mathbf{y = -5x - 1}\)
Example
Find the equation of the line joining the points A (3, 2) and B (-1, 10)
Solution:
Let the equation be \(y = mx + c\).
Values for m and c are to be found.
m is the gradient
\(\matrix{ & ~x & ~y \cr Coordinates~of~A & ~3 & ~2 \cr Coordinates~of~B & -1 & -0 \cr Subtract & \hline ~4 & -8}\)
Gradient = \(\frac{difference~in~y~values}{difference~in~x~values} = \frac{-8}{4} = -2\)
The gradient is -2
Put this value for m into the equation
\(y = -2x + c\)
To find the value for c, use the x and y coordinates of either of the points A or B.
Using the point A may be easier as both values are positive.
Substituting \(x = 3\) and \(y =2\) into the equation \(y = m-2x + c\)
\(2 = -2(3) + c\)
\(2 = -6 + c\)
\(c = 8\)
The equation of the line is \(\mathbf{y = -2x +8}\)
Question
What is the equation of the line joining the points (3, 15) and (-2, 0)?
Solution:
Let the equation be \(y = mx + c\)
m is the gradient
\(\matrix{ & ~x & ~y \cr & ~3 & ~15 \cr & -2 & -0 \cr Subtract & \hline ~5 & -15}\)
Gradient is \(\frac{15}{5} = 3\)
Gradient is \(m = 3\)
Gradient is \(y = 3x + c\)
Using (3, 15)
Gradient is \(15 = 3(3) + c\)
Gradient is \(15 = 9 + c\)
Gradient is \(c = 6\)
The equation of the line is \(\mathbf{y = 3x + 6}\)
Parallel lines
As mentioned in the introduction, parallel lines have the same gradient.
When written in the\(y = mx + c\) form, parallel lines have the same value of m.
Example
Which of these lines are parallel to the line \(y = 5x - 4\)?
- \(y = 4x + 5\)
- \(y - 5x = 3\)
- \(2y = 10x + 4\)
- \(y = 5 - 5x\)
Solution:
When written as \(y = mx + c\), m should = 5
- Not parallel тАГтАГ\(m = 4\)
- Parallel тАГтАГтАГ can be rearranged to give \(y = 5x + 3\)
- Parallel тАГтАГтАГ can be rearranged to give \(y = 5x + 2\)
- Not parallel тАГтАГ can be rearranged to give \(y = -5x + 5\)
Example
A straight line goes through the point (-10, -2) and is parallel to the line \(y - x = 8\).
What is the equation of this line?
Solution:
Let the equation of the unknown line be \(y = mx + c\)
Rearrange the equation \(y - x = 8\) to give\(y = x + 8\)
\(y = (1)x + 8\)
\(m = 1\)
Gradient of the unknown line is also 1 as they are parallel
Equation of line is \(y = x + c\)
To find the value of c, use the point (-10, -2)
\(-2 = 1(-10) + c\)
\(c = 8\)
Equation of the line is \(\mathbf{y = x + 8}\)
Question
A line goes through the origin and also goes through the point (3, - 8).
A second line is parallel to the first one and goes through the point (-2, 12).
Show that the equation of this line is \(3y + 8x + 20 = 0\)
Solution:
First line
To find m
\(\matrix{ & ~3 & -8 \cr & 0 & 0 \cr Subtract & \hline ~3 & -8}\)
Gradient = \(\frac{-8}{3}\)
Second line
Let the equation be \(y = mx + c\)
\(m= \frac{-8}{3}\) as it is parallel to first line
\(y= \frac{-8}{3}x + c\)
Use the point (-2, 12), ( x = -2 and y = 12)
\(12 = \frac{-8}{3}(-2) + c\)
\(c = \frac{20}{3}\)
Equation is \(y = \frac{-8}{3}x + {20}{3}\)
Multiply across by 3
\(3y = -8x + 20\)
Rearrange
\(3y + 8x - 20 = 0\)
Test yourself
More on M3: Algebra
Find out more by working through a topic