Expanding and simplifying
Two linear expressions can be expanded, and then simplified by collecting like terms, if there are any.
Linear expressions have no terms with power of 2 or higher.
For example,
15x ã 4y is a linear expression but 15x ã 4yôý is not.
Expanding and simplifying two linear expressions
Two linear expressions can be multiplied together by separating the terms in the first bracket and then multiplying each in turn by the terms in the second bracket.The expanded expression can then be simplified by collecting like terms.
Example
Expand the brackets and simplify fully \((p+ 3q)(3p ã 5q)\)
Solution
This time there are terms in ãpã and terms in ãqã with no stand-alone numbers, but the method is exactly the same.
\(\mathbf{p(3p - 5q) + 3q(3p - 5q)} = {3p^2- 5qp} +9qp - 15q^2{+ 3x - 12}\)
Remember that p x -5q = -5pq or -5qp
The order of the letters does not matter but the number always comes first.
\(3p^2 {- 5qp + 9qp} - 15q^2 = 3p^2 + 4qp - 15q^2\)
Answer
\((p+ 3q)(3p ã 5q) = 3p^2 + 4qp - 15q^2\)
Example
Expand and simplify \((2x - 3)(3x - 5)\)
Solution
Separate the ã2xã and the ã-3ã from the first bracket and multiply each by (3x - 5)
\(\mathbf {(2x -3)(3x - 5) = 2x (3x - 5) + 3 (3x - 5)}\)
Expand the brackets
\(\mathbf {{2x (3x - 5)}{- 3 (3x - 5)} = {6x^2- 10x }{- 9x - 12}}\)
Be careful with signs when multiplying out the second bracket!
Now collect like terms
\(6x^2 {- 10x + 9x} +15 = 6x^2 {-19x} + 15 \)
Answer
\((2x - 3)(3x - 5) = 6x^2 ã 19x + 15\)
Example
Expand the brackets and simplify fully \((p+ 3q)(3p ã 5q)\)
Solution
This time there are terms in ãpã and terms in ãqã with no stand-alone numbers, but the method is exactly the same.
\(\mathbf {p(3p - 5q) {+ 3q(3p - 5q)} = {3p^2- 5qp} +9qp - 15q^2 {+ 3x - 12}}\)
Remember that p x -5q = -5pq or -5qp
The order of the letters does not matter but the number always comes first.
\(3p^2 {- 5qp + 9qp} - 15q^2 = 3p^2 + 4qp - 15q^2\)
Answer
\((p+ 3q)(3p ã 5q) = 3p^2 + 4qp - 15q^2\)
Alternative FOIL method
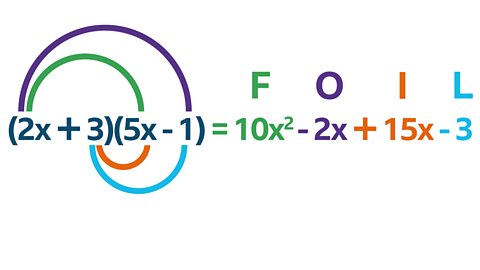
An alternative method is the FOIL method. It can be quicker especially if you are confident with + and ã numbers.
FOIL stands for
- First - Multiply the first terms in the brackets
- Outside - Multiply the outside terms
- Inside - Multiply the inside terms
- Last - Multiply the last terms
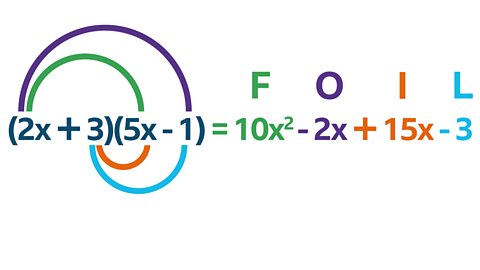
- Now collect like terms
\(10x^2 {- 2x + 15x} - 3 = 10x^2 {+ 13x} - 3\)
Answer
\((x + 3)(x - 4) = 10x^2 + 13x ã 3\)
Question
Expand the brackets and simplify this expression
(2y ã 7)(4y + 1)
Method 1
\((2y ã 7)(4y + 1) = 2y(4y + 1) -7(4y + 1)\)
\(= 8y^2 + 2y -28y ã 7\)
Collect like terms
\(= 8y^2 - 26y ã 7\)
Answer
\((2y ã 7)(4y + 1) = 8y^2 -26y ã 7\)
Method 2 - FOIL
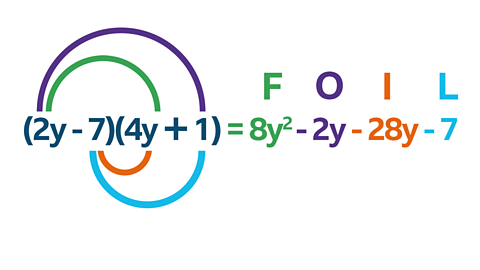
Collect like terms
\(8y^2 + \mathbf{2y -28y} ã 7 = 8y^2 \mathbf{-26y} ã 7\)
Answer
\((2y ã 7)(4y + 1) = 8y^2 -26y ã 7\)
Test yourself
More on M3: Algebra
Find out more by working through a topic
- count5 of 5