Quadradic equations
These topics provide useful background
Solving Quadratic Equations
The general form of a quadratic equation is
\(\mathbf{ax^2 + bx + c = 0}\)
where \(a\), \(b\) and \(c\) are numbers.
Both \(b\) and/or \(c\) can be equal to zero.
In this section, solving equations where \(a >1\) will be considered.
To solve a quadratic equation
- Rearrange the equation so that the Right Hand Side (RHS) = 0
- Factorise the Left Hand Side (LHS)
- Put the first factor equal to 0 and solve the linear equation
- Put the second factor equal to 0 and solve the linear equation
- Write down the two solutions
Example
Solve the equation \(2x^2 - x = 5x\)
Solution
Rearrange the equation so that the RHS = 0
\(2x^2 - x - 5x = 0\)
\( 2x^2 - 6x = 0 \)
Factorise the LHS
\(2x (x - 3) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(2x = 0\)
\(x = 0\)
Put the second factor equal to 0 and solve the linear equation
\(x - 3 = 0\)\( x = 3\)
Write down the two solutions
Solutions \(x = 3\) or \(x = 0\)
Answer:
\(x = 3\) or \(0\)
Question
Solve the equation \(\mathbf{5x^2 + 3x + 7 = 7 - x}\)
Solution
Rearrange the equation so that the RHS = 0
\(5x^2 + 3x + 7 = 7 - x\)
\(5x^2 + 4x = 0\)
Factorise the LHS
\(x(5x + 4) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(x = 0\)
Put the second factor equal to 0 and solve the linear equation
\(5x + 4 = 0\)\(x = -\frac{4}{5}\)
Write down the two solutions
\(x = 0\) or \(x = -\frac{4}{5}\)
Answer:
\(\mathbf{x = 0}\) or \(\mathbf{x = -\frac{4}{5}}\)
Example
Solve the equation \(\mathbf{3x^2 + 10x = 8}\)
Solution:
Rearrange the equation so that the RHS = 0
\(3x^2 + 10x - 8\)
Factorise the LHS
\(3x^2 + 10x - 8 = 0\)
\(Sum = +10\)
\(Product = -24\)
Remember: when \(a > 1\), in this case 3, the product is \(a \times c\), in this case \(3 \times -8 = -24\)
numbers are \(+12\) and \(-2\)
\(3x^2 + 10x -8 = 3x^2 +12x - 2x -8\)
\(= 3x (x +4) - 2 (x + 4)\)
\(= (3x - 2) (x + 4)\)
Equation becomes \((3x - 2) (x + 4) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(3x - 2 = 0\)
\(3x = 0\)
\(x = \frac{2}{3}\)
Put the second factor equal to 0 and solve the linear equation
\(x + 4 = 0\)
\(x = - 4\)
Write down the two solutions
\(x = \frac{2}{3}\) or \(x = -4\)
Answer:
\(\mathbf{x = \frac{2}{3}}\) or \(\mathbf {x = -4}\)
Question
Solve the equation \(\mathbf{4a^2 + 3a + 10 = 0}\)
Rearrange the equation so that the RHS = 0
No need to rearrange as RHS is already equal to zero
Factorise the LHS
\(4a^2 + 3a + 10 = 0\)
\(Sum = -3\)
\(Product = - 40\)
Key numbers are - 8 and + 5
\(4a^2 - 8a + 5a -10 = 0\)
\(4a(a - 2) + 5(a -2) = 0\)
\((4a - 5)(a -2) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(4a + 5 = 0\)
\(a = -\frac{5}{4}\)
Put the second factor equal to 0 and solve the linear equation
\(a - 2 = 0\)
\(a = 2\)
Write down the two solutions
\(a = 2\) or \(a = -\frac{5}{4}\)
Answer:
\(\mathbf{a = 2}\) or \(\mathbf{a = -\frac{5}{4}}\)
Example
Solve the equation \(\mathbf{9x^2 - 25 = 0}\)
Solution
Rearrange the equation so that the RHS = 0
No need to rearrange as RHS is already equal to zero.
Factorise the LHS
Use the difference of two squares
\((3x + 5) (3x - 5) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(3x + 5 = 0\)
\(x = -\frac{5}{3}\)
Put the second factor equal to 0 and solve the linear equation
\(3x + 5 = 0\)
\(x = +\frac{5}{3}\)
Write down the two solutions
\(x = +\frac{5}{3}\) or \(x = +\frac{5}{3}\)
Answer:
\(\mathbf{x = +\frac{5}{3}}\) or \(\mathbf{x = +\frac{5}{3}}\)
Alternative method
\(9x^2 - 25 = 0\)
Solution:
\(9x^2 = 25\)
Take the square root of both sides
\(3x = \sqrt{25}\)
\(x = \frac{\sqrt{25}}{3}\)
\(\sqrt{9x^2} = 3x\)
\(\sqrt{25} = +5 or -5\)
Don't forget the negative square root!
Answer:
\(\mathbf{x = +\frac{5}{3}}\) or \(\mathbf{x = +\frac{5}{3}}\)
Question
Solve the equation \(\mathbf{4a^2 - 81 = 0}\)
Solution
\(4x^2 - 81 = 0\)
\(4x^2 = 81\)
\(2x = \sqrt{81}\)
\(x = \frac{\sqrt{тИЪ81}}{2}\)
Answer\(\mathbf{x = + \frac{9}{2}}\) or \(\mathbf{x = - \frac{9}{2}}\)
Solution using DOTS
\((2x + 9) (2x - 9) = 0\)
\(2x + 9 = 0\)
\(x = -\frac{9}{2}\)
\(2x - 9 = 0\)
\(x = +\frac{9}{2}\)
Answer
\(\mathbf{x = + \frac{9}{2}}\) or \(\mathbf{x = - \frac{9}{2}}\)
Another way to write this answer is
\(\mathbf{x = \pm\frac{9}{2}}\)
Using the Quadratic Formula
A formula can be used to solve any equation in the form \(\mathbf{ax^2 + bx + c = 0}\).
If the quadratic expression can be factorised, it is generally quicker to use the factors method. However, if it cannot be factorised, or if the factors are not easily found, the formula is the way to go.
The formula is
\(\Large\mathbf{x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}\)
Values for a, b, and c are put into the formula to give values for x.
Example
Solve the equation
\(2x^2 + 6x - 1 = 0\)
First check that \(2x^2 + 6x - 1 = 0\) cannot be factorised.
There are no numbers that add to give \(+6\) and multiply to give \(-2\)
apply the formula:
\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)
In the equation, \(2x^2 + 6x - 1 = 0\)
\(a = +2\)
\(b = +6\)
\(c = -1\)
Always write down the values for a, b and c before applying the formula.Make sure each value is written as either + or -
Put these values into the formula
\(x=\dfrac{-6\pm\sqrt{6^2-4(2)(-1)}}{(2)(2)}\)
Use brackets around negative values. This should reduce mistakes with signs
\(x=\dfrac{-6\pm\sqrt{36+8}}{4}\)
\(x=\dfrac{-6\pm\sqrt{44}}{4}\)
\(x=\dfrac{-6+\sqrt{44}}{4}\)
\(x= 0.16\) (2 d.p.)
or
\(x=\dfrac{-6-\sqrt{44}}{4}\)
\(x= 3.16\) (2 d.p.)
If a degree of accuracy is not specified, use 2 decimal places
Answer:
\(x= 0.16\) (2 d.p.)
or
\(x= 3.16\) (2 d.p.)
Question
Solve the equation
\(3 + 4x - 2x^2 = 0\)
Give your answer to 2 decimal places.
Solution
The question asks for answers to 2 decimal places which means that the quadratic expression does not factorise and therefore the formula should be used.
Rearrange to give the more familiar \(ax^2 + bx + c\) order of terms.
\(2x^2 - 4x -3 = 0\)
\(a=2\)
\(b=-4\)
\(c=-3\)
Or use
\(a=-2\)
\(b=+4\)
\(c=+3\)
the outcome will be the same
Apply the formula
\(\mathbf{x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}\)
\(x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4(2)(-3)}}{2(2)}\)
\(x=\dfrac{4\pm\sqrt{(16+24}}{4}\)
\(x=\dfrac{4\pm\sqrt{40}}{4}\)
Answer:
\(x=\dfrac{4+\sqrt{40}}{4}\)
\(x=2.58\)
or
\(x=\dfrac{4-\sqrt{40}}{4}\)
\(x=-0.58\)
Forming quadratic Equations
Sometimes an equation has to be formed and then solved.
Forming the equation is an important part of the question and no marks will be awarded for skipping the equation and guessing an answer, even if it is correct.
To form the equation, think about what you would do if the information had been given in numbers and do the same with the algebraic terms.
Example
A rectangle measures \((x + 2)\) cm by \((2x -3)\) cm.
The area of the rectangle is 15 cm┬▓.
Form an equation and solve it to find the value of \(x\) and hence the length of the longer side.
Don't find a solution by trial and improvement
Solution
\(\text{Area of rectangle} = (x + 2) (2x - 3)\)
\(Area = 2x^2 + x - 6\)
Area was given as 15 cm┬▓ -
\(Area = 2x^2 + x - 6 = 15\)
Rearrange to have 0 on RHS
\(2x^2 + x - 21 = 0\)
Factorise
Product = -42
Sum = + 1
Key numbers are +7 and -6
\(2x^2 + x - 21 = 2x^2 + 7x - 6x -21\)
\(= x (2x + 7)- 3(2x + 7)\)
\(= (2x + 7) (x - 3)\)
\(2x + 7 = 0\)
\(x=-\frac{7}{2}\)
x cannot equal \(-\frac{7}{2}\) This would make the side measuring (2x -3) negative in length.
\(x - 3 = 0\)
\( x = 3\)
\(x + 2 = 5\)
\( 2x- 3 = 3\)
Answer:
\(x + 2 = 5\)
\( 2x- 3 = 3\)
Once an equation is formed and solved, check that the question is answered.Here, the answer is not 3, but 5 cm.
A quadratic equation usually has two solutions. In these types of questions, one of the answers will make sense and the other may not. Here, x =3 is the value you need to use.
Length of longer side is 5 cm.
Question
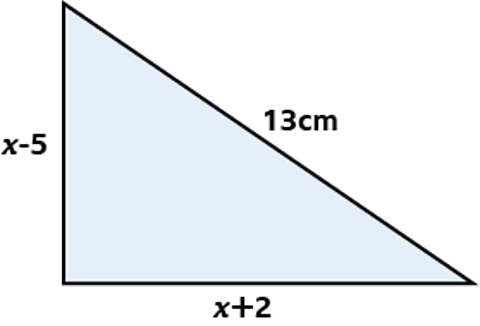
The diagram shows a right-angled triangle whose hypotenuse is 13 cm long. The other two sides are \((x + 2)\) cm and \((x тАУ 5)\) cm
Form an equation and solve it to find the lengths of the two unknown sides.
Solution
Use Pythagoras's Theorem
\((x - 5)^2 + (x + 2)^2 = 13^2\)\(x^2 - 10x + 25 + x^2 + 4x + 4 = 169\)
Time saving tip! \((x + a)^2 = x^2 + 2ax + a^2\)
Simplify LHS
\(2x^2 - 6x + 29 = 169\)
\(2x^2 - 6x - 140 = 0\) (├╖ everything by 2)
\(x^2 - 3x - 70 = 0\)
Factorise
Product = - 70
Sum = - 3
Key numbers -10 and 7
Solve
\((x + 7) (x - 10) = 0\)
\(x = -7\) тЬЧ Not possible
\(x - 10 = 0\)
\(x = 10\) тЬФ
Lengths of sides are \(x + 2 cm\) and \(x - 5 cm\)
\(x + 2 = 12\)
\(x - 5 = 5\)
Answer:
Lengths of unknown sides are 5 cm and 12 cm
Test yourself
More on M4: Algebra
Find out more by working through a topic