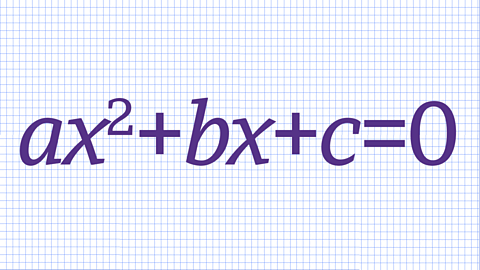������̳

Factorising an expression means finding the factors that multiply together to give that expression.

Useful topics:

Module 3 Factorising

Knowledge of how to factorise expressions of the form \(\mathbf{x^2 +bx +c}\) will help.

How to factorise an expression with no number in front of the \(x^2\)

For \(\mathbf{x^2 + 5x + 6}\), the first step is to find two numbers whose sum is 5 and whose product is 6

\(\mathbf{x^2 + \color{green}5x + \color{red}6}\)
\(\text{Sum} = \color{green}5\quad= 2 + 3\)
\(\text{Product} = \color{red}6\quad = 2 \times 3\)

This gives the factors with no further working.

\(\mathbf{x^2 + 5x + 6 = (x + 2)(x + 3)}\)

This method for factorising \(x^2 + bx + c\) can be modified to factorise \(ax^2 + bx +c\)

Example

Factorise \(\mathbf{3x^2 + 11x + 10}\)

Solution

Write down the sum and product to help find the factors.
The sum is \(11\) but because there is a \(3\) in front of the \(x^2\), the product needed is \(3 \times 10\)
(Number in front of the \(x^2\) times the number at the end)

Find two numbers whose sum is \(11\) and whose product is \(3 \times 10 = 30\)
\(5 + 6 = 11\)
\(5 \times 6 = 30\)

Rewrite the equation splitting up the middle term
\(3x^2 + \color{blue}{5x + 6x}\color{black} + 10\)

Factorise the first two terms \(\color{purple}{3x^2 + 5x}\color{black} + 6x + 10\)
\(= \color{purple}{x(3x + 5)}\color{black} + 6x + 10\)

Factorise the last two terms to leave 3x + 5 in the bracket \(\color{purple}{ = x(3x + 5)}\color{black} + 2(3x + 5)\)

Write down the factors
\(= (3x + 5)(x + 2)\)

Answer:

\(\mathbf{3x^2+11x+10 = (3x+5)(x+2)}\)

Example

Factorise
\(\mathbf{3x^2 - 5x - 2}\)

Solution:

Write down the sum and product
\(\text{Sum} = -5\)
\(\text{Product} = - 6\quad(3 x -2 = -6)\)

Find the two numbers that add to give the sum and multiply to give the product
\(-6 + 1 = -5\)
\(-6 \times 1 = -6\)

Rewrite the expression, splitting up the middle term
\(3x^2 \color{blue}-6x + x \color{black}-2\)

Factorise in pairs - to give the same expression in two brackets
\(= 3x \color{purple}(x - 2)\color{black} + 1 \color{purple}(x - 2)\)

Write down the factors
\(= (3x + 1)\color{purple}(x - 2)\)

Answer:

\(\mathbf{3x^2 – 5x - 2 = (3x + 1)(x - 2)}\)

The expression \(9x^2 – 25\) can be factorised using the Difference Of Two Squares method. (DOTS)

In this expression,
\(9x^2 = (3x)^2\)
\(25 = 52\) and there is a minus sign in between

The difference of two squares.
\(9x^2 – 25 = (3x + 5)(3x – 5)\)

In general,
\(a^2x^2 – b^2\) can be factorised to give \(\mathbf{(ax + b) (ax – b)}\)

Example

Factorise
\(4x^2 - 49\)

Solution:

\(4x^2 = (2x)^2 \text{and }100 = 10^2\) There is a \(–\) sign in between.

Use DOTS

The factors can be written down without any further working. \(4x^2 – 100 = (2x)^2 – 10^2\) \(= (2x + 10)(2x – 10)\)

Example

Factorise
\(9y^2 - 64x^2\)

Solution:

Use DOTS. \(9y^2 - 64x^2 = (3y)^2 – (8x)^2\)

Factors are
\((3y + 8x)(3y – 8x)\)

Answer
\(9y^2 - 64x^2 = (3y +8x)(3y - 8x)\)